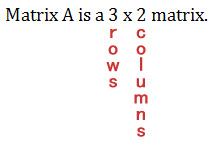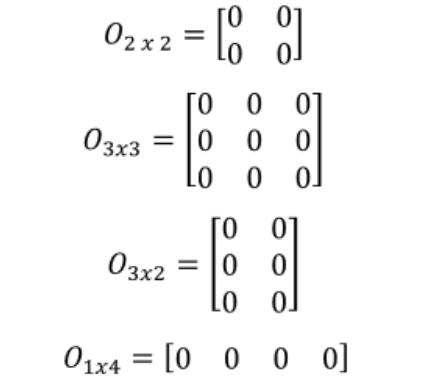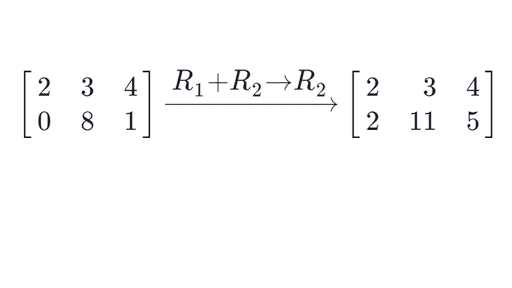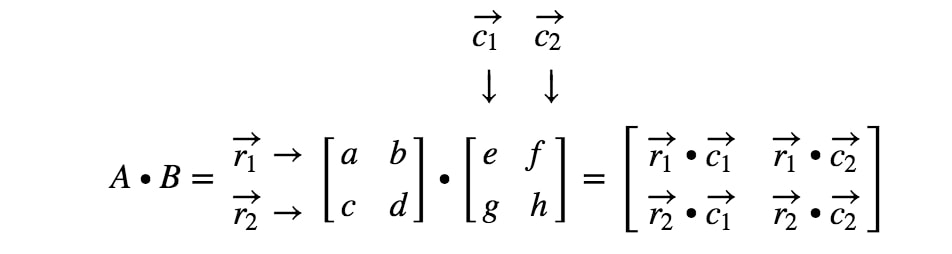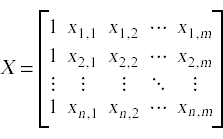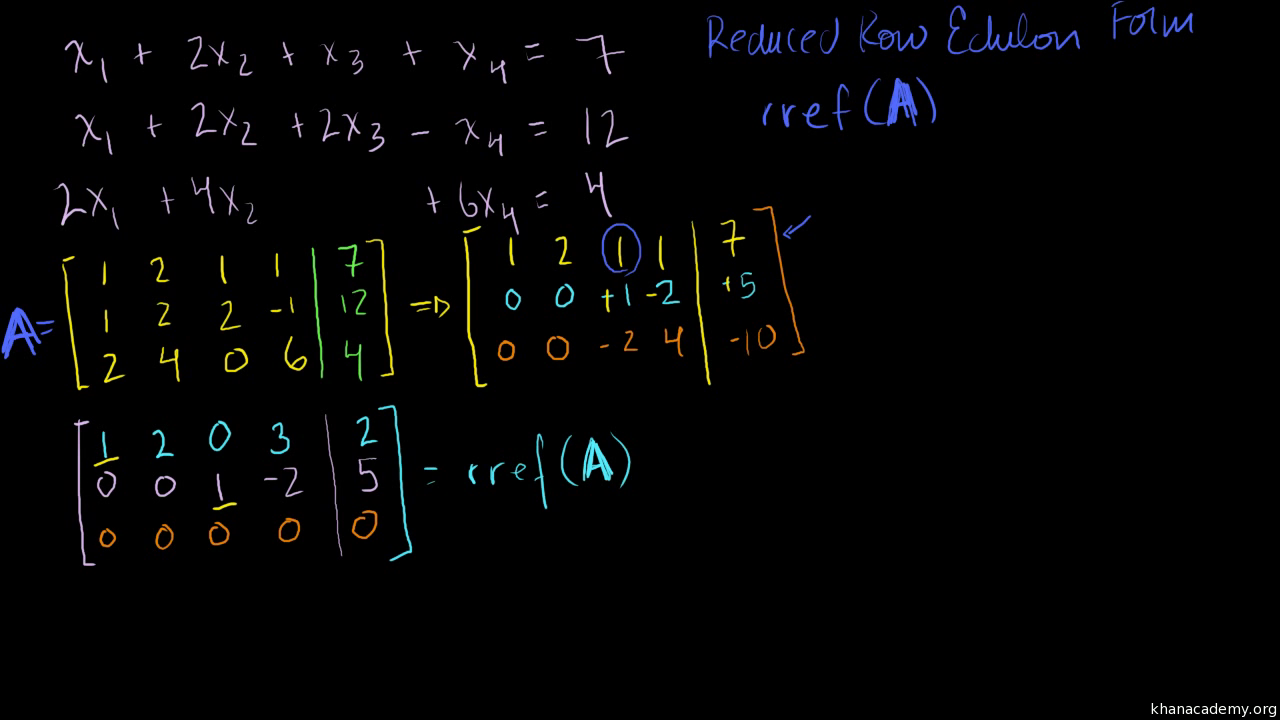2 X 1 Column Matrix

The dot product is performed for each row of a and each column of b until all combinations of the two are complete in order to find the value of the corresponding elements in matrix c. For example when you perform the dot product of row 1 of a and column 1 of b the result will be c 1 1 of. For another example if x is an n k 1 matrix and β is a k 1 1 column vector then the matrix multiplication xβ is possible.

wright furniture flooring and mattress hannibal mo 2 stage air compressor hvac 1 inch nylon rope woolite carpet and upholstery cleaner how to remove plastic tab 3mm sheet metal gauge worms that live in carpet work christmas party table names 1 1 2 waste pipe cap

Matrices Rows Columns Elements Solutions Examples Videos

Adding And Subtracting Matrices Chilimath

What Is Matrix Notation In Math Studypug

Matrices

Program To Find The Sum Of Each Row And Each Column Of A Matrix Geeksforgeeks

Matrix Multiplication How To Multiply Two Matrices Together Step By Step Visual Animation And Interactive Practice Problems

A matrix is a rectangular arrangement or array of numbers often called elements.

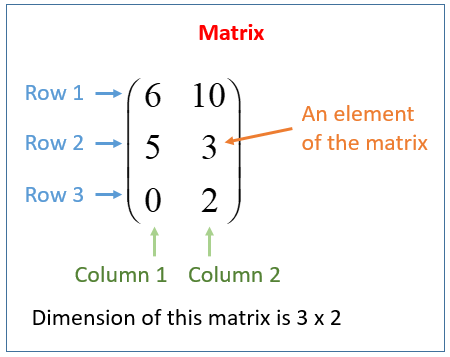
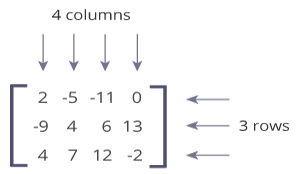
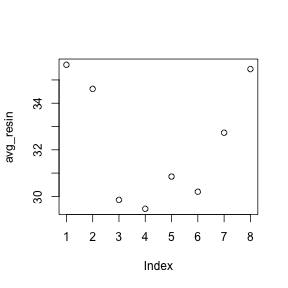
2 x 1 column matrix. Provided that they have the same size each matrix has the same number of rows and the same. For example the dimension of the matrix below is 2 3 read two by three because there are two rows and three columns. In linear algebra a column vector or column matrix is an m 1 matrix that is a matrix consisting of a single column of m elements. That is c is a 2 5 matrix.

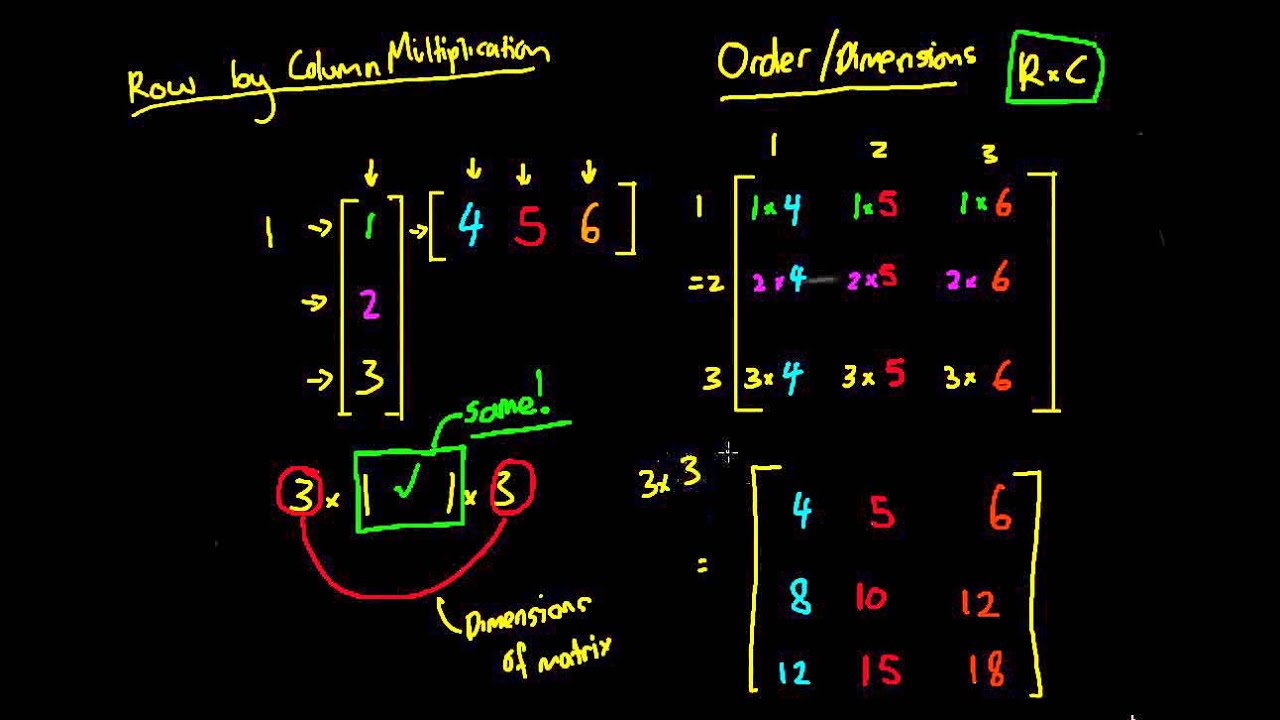
A 1 1 b 1 1 a 1 2 b 2 1 a 1 3 b 3 1 c 1 1. In mathematics a matrix plural matrices is a rectangular array or table see irregular matrix of numbers symbols or expressions arranged in rows and columns. Throughout boldface is used for the row and column vectors. In general the i j entry of a matrix a is written a ij and the statement.

The resulting matrix xβ has n rows and 1 column. A 2 4 1 2 ans 5 11 9 7 4 14. A matrix this one has 2 rows and 3 columns to multiply a matrix by a single number is easy. For example since the entry 2 in the matrix above is in row 2 column 1 it is the 2 1 entry.

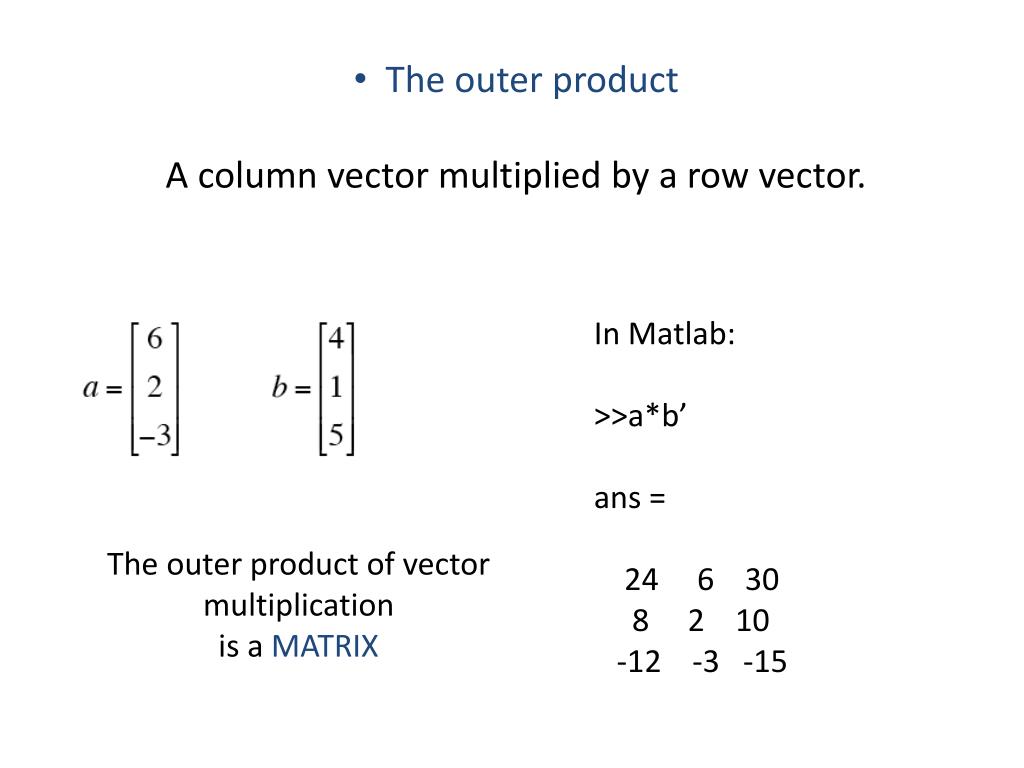
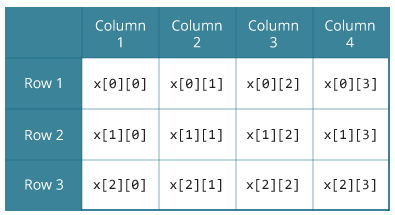
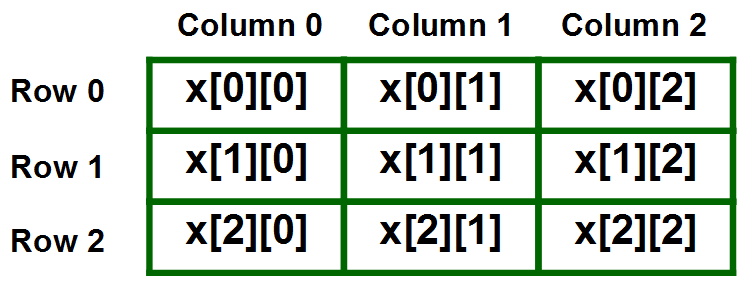
The size or dimensions m n of a matrix identifies how many rows and columns a specific matrix has. Similarly a row vector or row matrix is a 1 m matrix that is a matrix consisting of a single row of m elements. The resulting matrix c ab has 2 rows and 5 columns. The number of rows is m and the number of columns is n.

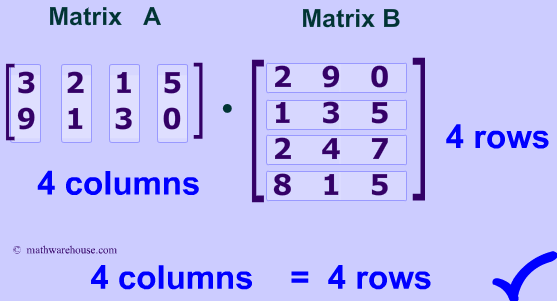
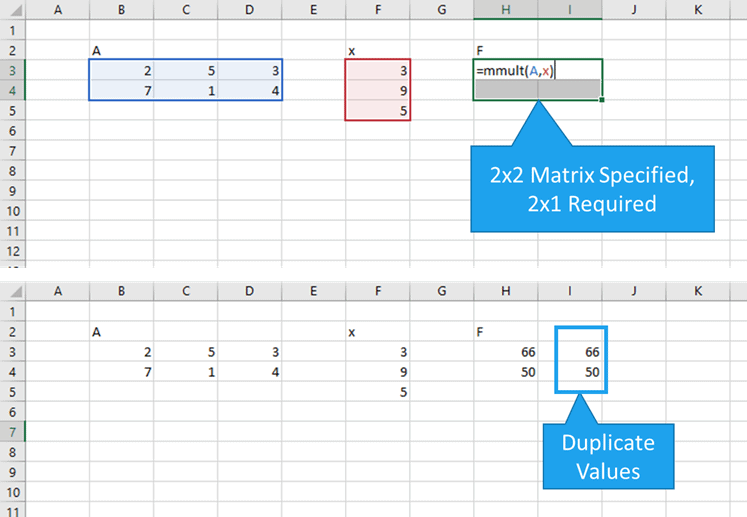
Note that the matrix multiplication ba is not possible. A 2 4 extract the element in row 2 column 4 ans 8 more generally one or both of the row and column subscripts can be vectors. Let us define the multiplication between a matrix a and a vector x in which the number of columns in a equals the number of rows in x. So if a is an m n matrix then the product a x is defined for n 1 column vectors x.

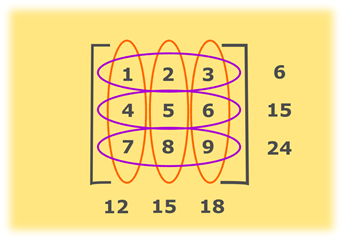
The dimension of a matrix must be known to identify a specific element in the matrix. Multiplying a matrix by another matrix. We call the number 2 in this case a scalar so this is called scalar multiplication. Indicates that a is the m x n matrix whose i j entry is a ij.

The 1 2 entry is 0 the 2 3 entry is 1 and so forth. The transpose indicated by t of a row vector is a column vector. These are the calculations.